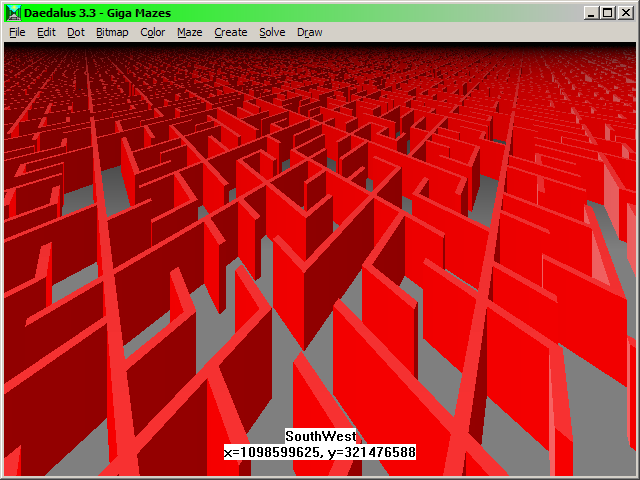

A virtual Maze in which the user is near cell coordinates X=1 billion, Y=321 million!
Introduction: What's the largest possible Maze? Mazes can be drawn by hand, but eventually you run out of patience or paper to make them larger. Similarly, Mazes can be constructed life size, but eventually you run out of money, building materials, or adjacent property to add on to them. Mazes can also be generated by computer, in which the computer can automatically create enormous Mazes very quickly. However, even there you eventually run out of computer memory, disk space, or processing time. Is there an alternate approach? Suppose we wanted to present a well-formed perfect Maze (unchanging and with a single solution and no loops or inaccessible locations) that measures a billion by a billion passages, or a Maze which is the size of the entire solar system? Yes, this can be done, through the concept of "virtual Mazes".
Definition: A "virtual Maze" is one where the whole Maze isn't stored in memory at once. The name is similar to "virtual memory", in which a computer can act as having more memory than actually available, by storing data that isn't being used at the time to disk. Virtual Mazes are similar to a Mandelbrot set fractal, in which the pictures within the Mandelbrot set exist virtually, and you just need to visit a particular coordinate at a high enough zoom level for them to reveal themselves. Games and graphics programs that present enormous worlds use a similar technique to render scenes, in which they only need to draw objects and polygons for objects nearby and visible to the player.
Viewport: A key part of implementing virtual Mazes is the "viewport". This is a section of the Maze being looked at, and which the computer actually generates the passages for. The viewport should always enclose the part of the Maze a user is looking at, or enclose the coordinates of a solver within the Maze. In addition, the user shouldn't ever be too close to the edges of the viewport, to ensure they can't look down a long passage and see any void area that hasn't been generated or "swapped in" yet. For example, only present the 100x100 cell section of passages or so nearest to your location, in a simulation in which you're walking through a large million by million passage Maze. Implemented correctly, presenting the 100x100 section won't take much longer than if the user were inside just a small 100x100 passage Maze to begin with. The result is experiencing a 1000000x1000000 passage Maze.
Implementation: Not all Mazes types or algorithms can be done as virtual Mazes. To be able to be expressed as a virtual Maze, it's necessary to be able to generate sections of it independently of each other in a consistent manner. That allows the virtual Maze algorithm to focus upon just the specified viewport area. Any work done outside of the viewport needs to be minimal enough and fast enough to not take too much processing time or memory. The user can move around within the viewport just like they can within a normal Maze of the viewport's size. However, when the user gets close enough to the edge of the viewport, the viewport should be moved so the user is closer to the middle of it. Regenerating or "swapping in" the new section of Maze being viewed should only result in a brief delay occasionally, as the user moves around.
Random numbers: All computer generated random Mazes make use of a random number generator. A random number generator can be initialized with a "seed", which determines the sequence of random numbers that follow. Given the same starting random number seed, the same Maze will be produced. To ensure a virtual Maze remains consistent and never changes as you move around, there should be a formula to determine a random number seed for each coordinate at each nesting level. The easiest way to accomplish this is with a quality random number generator that can take a set of data or multiple input numbers as the seed. For example, initialize the random number generator with the current coordinates, nesting level, and finally an actual seed number that's constant to distinguish different virtual Mazes from each other.
Note in the standard "C" programming language, the "rand()" function is not sufficient, because the "srand()" function to set the random number seed only takes a single 32 bit number to initialize the seed, which only gives 4 billion unique possibilities for initialization, which isn't extensive enough to cover the needs of large virtual Mazes. Instead, use a better random number generator such as the Marsenne Twister, since it has a very long period before repeating, and can be initialized with arbitrary length inputs. Daedalus uses a Marsenne Twister random number generator as of version 3.1 released in 2015.
3D: Virtual Mazes can be done in 3D as well as 2D. For 3D virtual Mazes, have a 3D viewport consisting of a cube of passages surrounding the viewing point.
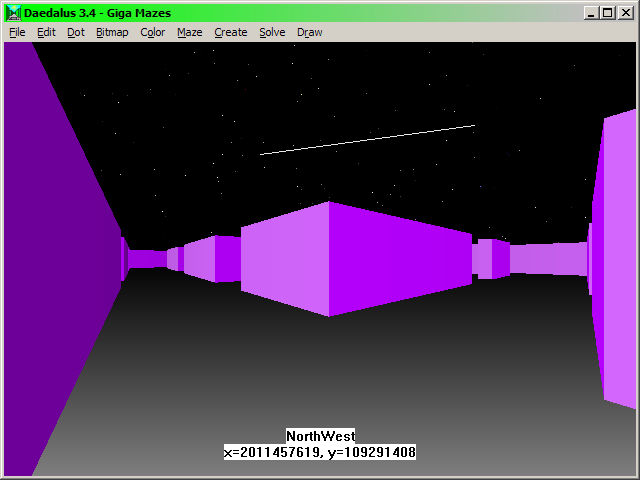
A virtual Maze in which the user is near cell coordinates X=2 billion, Y=109 million!
All of the below virtual Maze types are available in the program Daedalus, inside its "World's Largest Maze" applet. The "smallest" Maze produced by this applet is 2D and measures a billion by a billion passages (10^18 or one quintillion cells total) which if life sized (with passages 5 feet wide) it would cover the Earth's surface 4553 times. The largest version of this Maze is 3D and 2136750624 by 2136750624 by 2136750624 passages (215^4 power on each side) which adds up to 9,755,769,223,915,823,997,746,970,624 cells total (over 9.7 octillion), and if life sized (with tunnels 5 feet wide) it would fill the entire Earth's volume 30,246,426 times (over 30 million). If this 3D Maze were flattened into 2D, it would measure over 1000 AU (Astronomical Units) on a side, which is enough to cover the entire solar system 625 times (Pluto's orbit is only 80 AU wide). Stretched out in a single line, all the passages in this Maze would measure over 1.5 trillion light years, which is longer than the entire Universe (which is "only" 93 billion light years wide. ;-)
Nested cell: This is a version of the nested cell fractal Maze generation algorithm, applied in a virtual manner. In other words, create an X by Y Maze, and then generate nested X by Y Mazes within each cell. This nesting produces a fractal pattern, making this type a virtual fractal Maze. Consider a 10^9 by 10^9 passage Maze, or a 10x10 Maze nested with 9 levels total. If we want at least a 100x100 section around us, then we only need to create the 100x100 passage submaze at the lowest level, and the seven 10x10 Mazes it's nested within, to know exactly where all walls lie within a 100x100 section. (Actually it's best to have four adjacent 100x100 sections forming a square, in case you're near the edge or corner of a section looking down a passage into another section, but the same concept applies.) Nested cell Mazes can be done in both 2D and 3D, so both 2D and 3D virtual Mazes of this type are options.
Recursive division: This is a version of the recursive division Maze generation algorithm, applied in a virtual manner. This is similar in logic to nested cell above, except the nested sections are randomly sized. Instead of always making fixed cell size Mazes with Mazes of the same size within each cell, recursive division divides the given area randomly into a random sized 1x2 or 2x1 Maze. The virtual version of this algorithm only needs to recursively generate halves of the Maze which intersect the viewport rectangle. Recursive division Mazes can be done in both 2D and 3D, so both 2D and 3D virtual Mazes of this type are options.
Binary tree: This is a version of the binary tree Maze generation algorithm, applied in a virtual manner. Because every cell in a binary tree Maze is independent of every other cell, it's easy to generate just a section of a binary tree Maze, and therefore implement it virtually. Binary tree Mazes can be done in both 2D and 3D, so both 2D and 3D virtual Mazes of this type are options.
Bisection unicursal: This is a version of the passage bisection method of unicursal Maze generation, applied in a virtual manner. These unicursal Mazes are generated by taking a normal Maze, and bisecting each passage to get unicursal passages. To have the entrance of the unicursal Maze at one corner and the exit at the opposite corner, it's necessary to have a long passage along two adjacent edges of the standard Maze used to compose it. The standard Maze also needs to be able to be created virtually. The binary tree algorithm meets both criteria, so virtual unicursal Mazes can be created by bisecting virtual binary tree Maze passages. The bisection method of unicursal Maze generation can only be applied to 2D Mazes, so this is only available in 2D virtual Mazes.
Hilbert curve: This is a version of the Hilbert curve unicursal Maze generation, applied in a virtual manner. Quadrants of a Hilbert curve can be generated independently, so the section of it within a viewport can be quickly produced. There are no random numbers involved in producing Hilbert curve patterns, so that area is not a concern. Hilbert curves can be drawn in 2D squares or 3D cubes, so both 2D and 3D virtual Mazes of this type are options.
Classical Labyrinth: This is a extension of generating a classical Labyrinth, applied in a virtual manner. The classical seven circuit Labyrinth can be expanded to any number of rings that's one less than a multiple of four, e.g. 3, 7, 11, 15, and so on circuits. These Labyrinths can also be drawn in a square orthogonal manner. It's not difficult to only draw those walls which intersect a viewport. There are no random numbers involved when drawing these Labyrinth patterns, so that area is not a concern. The classical Labyrinth is a 2D pattern, so this is only available in 2D virtual Mazes. In Daedalus, these virtual Labyrinths can range from 499,999,999 to 1,068,375,311 circuits (half a billion to 1.06 billion circuits).

"Virtual Mazes" as described above only need to generate the parts of the Maze actually being looked at, which means they don't ever generate the entire Maze. These Virtual Mazes should be distinguished from standard Mazes that make use of a computer's virtual memory. In the latter case, the entire Maze gets generated, so you're still limited by disk space and processing time, however the virtual memory and disk space still allows generating Mazes much larger than can fit into memory all at once.
Mazes can be file based, when means they're stored in one or more files. For example, instead of one large bitmap, there's a grid of smaller bitmaps which together compose the entire Maze. Added together, these files can be too large to all fit in memory at once. However, just one of those files (or a 2x2 section in case the user is viewing coordinates near the edge of a section) can be loaded and displayed.
For file Mazes, the Maze generation process works similarly to the later viewing process, in which Maze sections are "swapped in" when needed, edited, and then saved back out when it's necessary to move to another section. File Mazes can only efficiently be done for those algorithms that never (or at least rarely) jump around when accessing the Maze. That means that when a cell is accessed, subsequent cells accessed will always (or at least usually) be nearby. That avoids missing the "cache" of the Maze in memory, and having to load or "swap in" parts of the Maze from disk too often. Here are three algorithms which work well as file Mazes. In Daedalus, all three file based Maze algorithms are available in its scripting language, with an example in the "virtual.ds" script that comes with the download:
Hunt and Kill: The Hunt and Kill algorithm usually only accesses adjacent cells during the creation process, which makes it a good option for file based Mazes. Note that "hunt" mode is best done in a spiral pattern from the start point (instead of something like row by row which is easier implemented) in order to stay within the current swapped in section for as long as possible.
Example: I did a file based Maze using Hunt and Kill when generating the giant Maze printout pictured. That Maze measures 1023x2047 passages (2 million cells) within a 2048x4096 pixel bitmap. A 2048x4096 pixel bitmap contains 8 million bits total, or exactly one megabyte (1048576 bytes or 1024K). That doesn't seem like much today, however I generated the Maze back in 1987 on a TRS-80 CoCo computer with only 64K of available RAM. How does one fit a 1024K Maze within just 64K of RAM? The answer of course was to store it on disk. However, the 5.25" floppy disks at the time only stored 156K of data per disk side, so I used eight such disks (storing 128K of Maze data on the front and back of four different disks). The computer would work on the data within 64K, and when needing to access a neighboring section would save the data to disk, and then load data from disk for the next section. However, eventually (on the order of once every few minutes) it would need data from a different disk, and the program would stop and ask me to flip the disk over or stick in a different disk (I only had a single drive system). That would require babysitting the program to manually give it the disks it needs, making the process take multiple days to finish. Today, Daedalus can easily generate a 1023x2047 passage Maze entirely within memory on even older PC's in just a fraction of a second, which shows how much computers have advanced in just a few decades! ;-)
Aldous Broder: The Aldous Broder algorithm only ever accesses adjacent cells during the creation process, which makes it a good option for file based Mazes.
Recursive backtracking: Recursive backtracking is similar to Hunt and Kill, in that carving always accesses an adjacent cell, and similarly popping the stack always accesses adjacent cells as well. However, if the Maze is large enough, eventually even the stack becomes too large to fit in memory all at once. However, the stack also fits the adjacent accessing quality, because one only ever accesses the current top of the stack, which means the stack can be file based too. When the stack becomes too large, the earlier parts of it are saved to disk, and only the part near the top of the stack is kept within memory.

Section of an infinite length Maze, in which the bottom half is being generated.
Why stop at just extremely large Mazes? Why not have a truly infinitely large Maze? Yes, this is possible! ;-) There are two ways to have "infinite" sized Mazes on a finite computer. One is an effectively infinite Maze that can continually be added on to forever, until one decides to end it. The other is a fractal Maze truly defined in terms of itself.
Infinite length Mazes: An infinite length Maze is one that has a constant width, and a length that can be arbitrarily long. Such Mazes are generated by only keeping part of the Maze in memory at a time and "scrolling" from one end to the other, in which earlier rows are printed and discarded while later rows are created. Infinite Mazes can be produced using a few different algorithms. Daedalus supports creating infinite Mazes with commands on the "Create / Infinite" menu.
Recursive fractal Mazes: A recursive fractal Maze is a Maze which is defined to contain copies of itself. That means recursive fractal Mazes are effectively infinite sized, since they feature infinitely long dead ends. They are described more below.
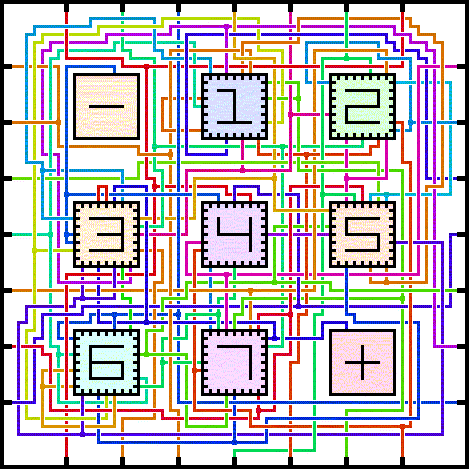
A recursive fractal Maze containing seven copies of itself, in which you start at the "-" and finish at the "+".
A "fractal Maze" is a Maze composed of smaller Mazes. In other words, a fractal Maze has fractal qualities, in which sections within the Maze have similar properties to (or even contain identical copies of) the Maze as a whole. Daedalus can generate several different types of fractal Mazes:
Nested cell fractal Mazes: A nested cell fractal Maze is a Maze with other Mazes tessellated within each cell, in which the process may be repeated multiple times. Nested cell fractal Mazes can be done virtually to produce truly enormous but still finite Mazes, as described above. Daedalus can create nested cell Mazes with the "Create / Pattern / Nested Fractal" command.
Recursive fractal Mazes: A recursive fractal Maze is a true fractal, in which the Maze is actually defined to contain copies of itself. That means recursive fractal Mazes are effectively infinite sized, since they feature infinitely long dead ends within the recursively nested copies. However, a recursive fractal Maze can seem repetitive, since repetition of the main passages is what creates the infinite effect. Daedalus can create and automatically solve recursive fractal Mazes, and an example of one of these Mazes was featured on the CBS television show "Numb3rs".
Another example of a recursive fractal Maze can be seen here, which is (c) 2003 by Mark J. P. Wolf, and was featured on Mathpuzzle.com. A smaller (yet harder) recursive fractal Maze can be seen here, from the forthcoming book "100 Enigmatic Puzzles".
Recursive division algorithm: The recursive division algorithm is similar to nested cell fractal Mazes, in that the Maze is composed of cells, with smaller Mazes nested within each cell. However, here the Maze is composed of random sized cell 1x2 or 2x1 Mazes, with smaller random sized Mazes within each cell. Like nested cell, the results of this algorithm have fractal properties too, so recursive division can be considered a type of fractal Maze. Daedalus can create Mazes of this type with the "Create / More Perfect / Recursive Division" command.
Crack Mazes: Crack Mazes are formed by long lines crossing much of the Maze, followed by increasingly smaller lines between them, which looks like the surface of a leaf. That has fractal properties too, so Crack Mazes can be considered a type of fractal Maze. Daedalus can create Crack Mazes with the "Create / Crack" command.